Programming Assignment 2 Instructions
Due by February 11, 2019 11:55 pm
Goal: In this assignment, we will experiment with three different algorithms to train a linear regression models: solving normal equations, batch gradient descent, stochastic gradient descent.
Input Format: The datasets are given in tvs (tab-separated) format. The file format is:
- 1st row: the numer of data points N.
- 2nd row: the number of features D.
- 3rd row: the first column is the label, and following columns are feature names.
- N following rows: each has (D+1) columns where the the first column is the label and following D columns are features.
An example file can be found here. There are two dataset that we will work with in this assignment.
- data_10k_100.tsv: This dataset contains 10,000 points, each with 100 features.
- data_100k_300.tsv: This dataset contains 100,000 points, each with 300 features.
The dataset can be downloaded from here.
Output Format: output must be given in tsv format, with (D+1) columns and two rows:
- The first row is the coefficient names of the linear regression model. The first D columns contain w1, w2 up to wD, where wi is the coefficient of the i-th feature. The bias term, named w0, is in the last column.
- The second row contains values corresponding to the coefficents of the regression model.
The sample output for the sample dataset above can be downloaded here.
There are three questions in this assigment. The first and second question are worth 10 points each where the third question is worth 30 points, all of 50 points total.
Question 1 (10 points): Implement the algoithm that solves the normal equation to learn linear regression models. For full score, your algorithm must run in less than 1 minutes on the dataset data_100k_300.tsv, with the loss function value less than 70.
Question 2 (10 points): Implement the batch gradient descent algorithm, with T = 200 epochs, learning rate η = 0.000001 (this is 10-6). For full score, your algorithm must run in less than 5 minutes on the dataset data_10k_100.tsv with loss value less than 270,000 (this is 27x104).
Question 3 (30 points): Implement the stochastic gradient descent algorithm with:
- T = 20 epochs, learning rate η = 0.000001 (this is 10-6) and batch size m = 1 on the dataset data_10k_100.tsv. For full score, your algorithm must run in less than 1 minutes with loss value less than 30.
- T = 12 epochs, learning rate η = 0.0000001 (this is 10-7) and batch size m = 1 on the dataset data_100k_300.tsv. For full score, your algorithm must run in less than 10 minutes with loss value less than 70.
Each part in question 3 is worth 15 points.
Note 1: Submit your code and output data to the Connex
FAQ
Q1: Can I use libarary for computing matrix inversion in Question 1.
Answer: Yes. You are allowed Numpy in question 1. You can also use Numpy for other questions as well.
Q2: How do I initiate the weight vector for gradient descent?
Answer: I initiat the weight vector randomly where each component is drawn from [0,1] randomly using numpy.random.random_sample()
Q3: What loss function should I use?
Answer: For all questions, you should use this loss function: 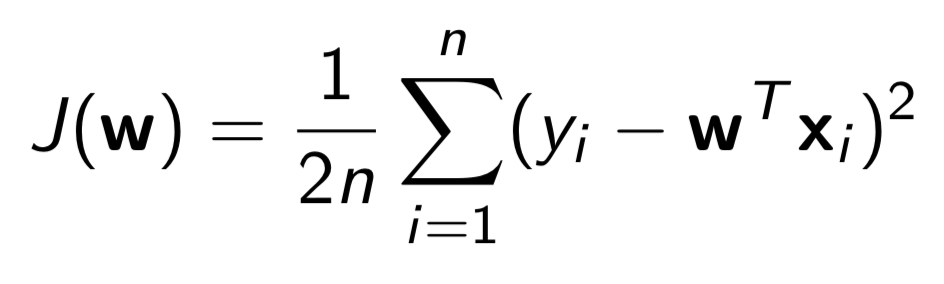
Want to go back to the course overview, click here.